|
|
|
| 英文版线性代数（linear Algebra)基础知识要点：线性方程组(Systems of Linear Equations)，线性变换(Linear Transformations)，矩阵和行列式(Determinant)，特征值(Eigenvalue)和特征向量(eigenvector)，矩阵相似对角化(Diagonalization)和合同对角化，正交投影(orthogonal Projection)等 |
| 英文版线性代数（linear Algebra)基础知识要点 |
|
| 题关键词：配方法，以及特征值法划二次型成标准型，并求其符号或判定正定性。 |
题： |
 |
|
| 题关键词：不可对角化矩阵，相似于他的约当标准型矩阵，约当标准型要根据特征值和特征向量和相似的定义综合取定 |
|
|
|
题关键词：二次型及其矩阵， 二次型惯性指数与规范型
|
设A为n阶实对称矩阵，秩r(A)=n，Aij是A=(aij)nXm中元素的代数余子式，二次型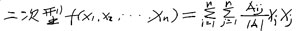 （1）记X=（x1,x2,...,xn)T, 把f(x1,x2,...,xn)写成矩阵形式，并证明二次型f(X)的矩阵为A-1 |
|
|
| 题关键词：矩阵特征值(eigenvalues)的特征向量(eigenvectors)的定义，矩阵特征值与其伴随阵和逆阵的特征值的关系。 |
题：Let A be a 3X3 matrix and its eigenvalues are λ1= 1, λ2= 2, λ3= 3,then
Find :
(1) det(A), (2) the eigenvalues of A -1 (3) the eigenvalues of adj(A),
(4)the eigenvalues of A-1+A2 (注：det(A)=|A|, adjA = A* ) |
|
|
| 题关键词：矩阵相似(similar)与合同(contract)，方阵对角化(diagonalization) |
| 设A为三阶矩阵，P=(α1,α2,α3)为3阶可逆矩阵，Q=(α1,α2,α3+α2)，(1)若PTAP=diag(1,1,2), 则QTAQ=？(2)若P-1AP=diag(1,1,2)，则Q-1AQ=？ |
|
|
| 题关键词：eigenvalues and eigenvector, diagonalization, inner product, invertible matrix. |
In this question A is the matrix A:=UVT , where u and v are non-zero vector in R10 .
1. If u·v≠0 find all 10 eigenvalues and describe their corresponding eigenvectors
a).Decide if A is diagonalizable.
b). Decide if A is invertible.
2. If u·v≠0 find all 10 eigenvalues and describe their corresponding eigenvectors
a).Decide if A is diagonalizable.
b).Decide if A is invertible.
|
|
|
| 题关键词：the matrix of the linear transformation，change of basis,linear maping, similar matrix. |
Let SєL(v,v) be given by S(u1)=u1-u2 , S(u2)=u1 , where ｛u1,u2｝is a basis for V.
Find the matrices of S with respect to the basis ｛u1,u2｝and with respect to the new basis｛w1,w2｝where w1=3u1-u2, w2=u1+u2.
Find invertible matrices X in each case such that X-1AX=B where A is the matrix of the transformation with respect to the old basis, and B is the matrix with respect to the new basis. |
|
|
| |
| |
| |
|
