| 题关键词:函数分段点处求导,导数定义,多阶可导性证明,演绎推理法,先证一般性,再应用到具体个例。 |
题: |
 |
|
| 题关键词:特征方程和特征根,齐次方程常数变异法解对应非齐次微分方程。 |
题: |
 |
|
| 题关键词:三角有理函数积分,诱导公式变换被积分式,然后凑配成易积分的形式。 |
题: |
 |
|
| 题关键词:配方法,以及特征值法划二次型成标准型,并求其符号或判定正定性。 |
题: |
 |
|
| 题关键词:比值法,比较法,积分法等常用判别无穷级数敛散性的例题 |
题:判断下列级数的敛散性
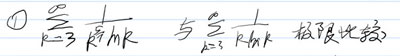  |
 |
|
| 题:柯西中值定理,拉格朗日中值定理 |
题:函数f(x)在【a,b】上连续,在(a,b)可导,且f ’(0)=0
 |
 |
|
| 题:积分中值定理,微分中值定理和介值定理 |
题:设函数f(x)在【0,3】上连续,在(0,3)内存在二阶导数,且2f(0)=积(0-2)f(x)dx=f(2)+f(3)
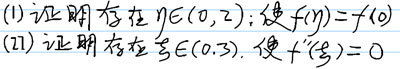 |
 |
|
| 题:坐标变换计算二重积分,雅克比行列计算。 |
计算: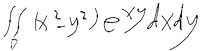 ,其中D是由经xy=1,xy=4和y=x,y=x+2围成的区域 ,其中D是由经xy=1,xy=4和y=x,y=x+2围成的区域 |
 |
|
题关键词: 方程组表示的空间曲线的切线及法平面方程,方程组表示多元隐函数求导。
|
| 题:求由x2+y2+z2-3x=0和2x-3y+5z-4=0决定的曲线在点(1,1,1)处的切线及法平面方程。 |
 |
|
| 题关键词: 多元函数极限定义及应用定义证明极限,夹逼定理和极坐代换求多元函数极限。 |
题:证明下列极限:
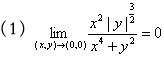   |
 |
|
| 题关键词:多元隐函数求偏导,空间切平面方程,两平面夹角与法向量夹角之间关系。 |
| 题:求旋转椭球面3x2+y2+z2=16上点(-1,-2,3)处的切平面方程和它与XOY面的夹角的余弦。 |
 |
|
| 题关键词:直角坐标空间曲线的切线和法平面方程求法,多元隐函数求偏导,克莱默法则解微分方程组。 |
| 题:求由x2+y2+z2-3x=0和2x-3y+5z-4决定的曲线在点(1,1,1)处的切线方程及法平面方程 |
 |
|
| 题关键词:用二重积分计算体积,用极坐标代换计算二重积分。 |
| 题:计算两两垂直相交的三个半径为a的圆柱的(三中心轴线相交于一点)时相交部分体积。 |
 |
|
| 题关键词:一阶线性常系数齐次/非齐次微分方程组,矩阵函数在微分方程组中的应用,矩阵指数函数 及其在解微分方程组中的应用。 |
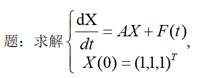 其中, 其中,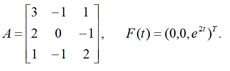 |
 |
|
| 题关键词:换元积分法,定积分性质,定积分换元 |
题:a) 利用换元积分法证明  b)并利用上式求 b)并利用上式求 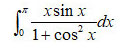 |
 |
|
| Problem:The extrema of the function of two or more variable, Ctitical point, Lagrange Multipliers, Max-Min Existence Theorem. |
| Let f(x,y)=y2-2y-3yx2 . (a) Find the critical points of f(x,y). (b) Find the absolute maximum and minimum values of f on the closed and bounded set enclosed by x=√y , x=1andy=0. |

|
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |



